Sulla costruzione di algoritmo di riconoscimento visivo
Avrete certamente notate la mia più che settimanale assenza. Purtroppo sono stato impegnato per motivi lavorativi: per farmi perdonare, ho deciso di produrre un bell’articolo (con tanto di programma Python) su un argomento iper attuale: la Machine Vision.
Intro
La Machine Vision raccoglie tutte le tecniche algoritmiche per il riconoscimento automatico di immagini. In essenza, utilizzando queste tecniche, è possibile insegnare ad una macchina a riconoscere gli oggetti più disparati (anche in tempo reale): l’applicazione più semplice é ad esempio la lettura automatica di testi. Come quando vi arriva la multa a casa, perché siete entrati come dei fessi nella ZTL: la telecamera, partendo da una foto, ha automaticamente letto la targa del vostro carro.
La teoria
A prima vista potrebbe sembrare che algoritmi di tale portata possano essere complessi e sostanzialmente distaccati dalla teoria di Data Science. In realtà, l’algebra lineare è ancora una volta onnipresente e viene in aiuto. Difatti, i metodi di Machine Vision non differiscono di molto dai metodi di Data Science in generale. Le differenze più marcate sono in come i dati (i.e. le immagini) vengono pre-processate, prima di essere inviate ad un classificatore (e.g. una Random Forest o una Rete Neurale).
Ordunque, qual’è la logica generale da seguire? Le immagini presentano un inevitabile problema di fondo: sono “pesanti” dal punto di vista di utilizzo memoria. Infatti, anche una piccola foto in b\n di dimensioni (in pixel) 100×100 rappresenta, per un calcolatore, una matrice di 10.000 elementi. Triplicate il valore per una in RGB.
Dunque, a meno di avere a disposizione una elevata potenza di calcolo, il classificatore impiegherà un tempo non trascurabile per stimare tutti i parametri.
Per ovviare a questo problema, non si deve nutrire il modello con le immagini pure, ma bisognerà estrarre delle misure (in inglese features) che riassumano l’informazione contenuta in esse. Di queste misure ne esistono di tutti i gusti ed è sostanzialmente impossibile riassumerle tutte. Come esempio, si prendano quelle utilizzate nel programma descritto più avanti nell’articolo.
Le features diventano dunque le nostre nuove variabili. In linea generale, il nostro problema viene nuovamente ridotto al generale:

dove X è un vettore di lunghezza p contenente i valori per le p misure e 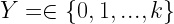 rappresentante le k classi di immagini.
rappresentante le k classi di immagini.
Un semplice esempio per chiarire: costruiamo un algoritmo per permettere al computer di riconoscere il colore blu dal rosso e viceversa, utilizzando immagini di 10×10 pixels. In questo caso avremo n immagini, alcune completamente rosse e altre blu. Per n abbiamo scelto 120.
Innanzitutto, importiamo le librerie che ci serviranno:
from PIL import Image
import numpy as np
import os
from os import walk
from sklearn.ensemble import RandomForestClassifier as RF
from sklearn import cross_validation
Ora doppiamo si procede con la creazione delle cartelle e delle immagini. Al tempo stesso si deve anche creare il vettore della variabile dipendente (indicato con Y).
# -------------------------------------------------------------------------------------- #
# Controlla l'esistenza di due cartelle per salvare le immagini. Se non presenti, le crea
directories = ["/foo/rosso/", "/foo/blu"]
for dir in directories:
if not os.path.exists(dir):
os.makedirs(dir)
# -------------------------------------------------------------------------------------- #
files = []
t = 0 # contatore
size = 10 # dimensione k, in pixel, di immagini kxk
iterations = range(0, 60) # costruisce 60 immagini
Y = []
for u in iterations:
k1 = int(np.random.uniform(0, 100)) # Valori aleatori per introdurre variabilità nei colori
k2 = int(np.random.uniform(0, 100))
k3 = int(np.random.uniform(0, 100))
k4 = int(np.random.uniform(0, 100))
col = [["rosso/", (255, k1, k2)], ["blu/", (k3, k4, 255)]] # paletta colori
for n,i in col:
im = Image.new("RGB", (size, size))
pix = im.load()
for x in range(size):
for y in range(size):
pix[x, y] = i # setta il colore dei pixel
filename = directory + n + str(t) + ".png"
im.save(filename, "PNG")
files.append(filename) # crea la lista dei filenames
Y.append(n[0:-1]) # Crea il vettore variabile dipendente con le classi
t += 1
Una volta creato il dataset e la variabile dipendente, si può procedere all’estrazione delle misure, che andranno a creare la nostra matrice X delle variabili indipendenti. Come già accennato, la scelta di quali features includere è notevolmente specifica al problema da risolvere. In questo semplice esempio, la distribuzione dei colori dei pixel sui 3 canali (RGB) è sufficiente.
Nota tecnica: nell’ultimo passaggio logico, se in R, sarebbe meglio vettorizzare la funzione anziché evocarla in loop. Ma usando Py, il for non crea troppi problemi.
print("Extracting features")
def extract_features(path):
''' Extract features from image of MetroBank Clapham Junction: colours distributions, sdev of the colours, number
of objects and several measurements on those objects.
Input: path - string with path of the picture
Output: a vector '''
# Resizing to 1000x1000, pixel distribution for each colour channel according to a fixed number of bins
im = Image.open(path)
im_arr = np.array(im)
hist_R = np.histogram(im_arr[:, :, 0].flatten()) # Distibuzione Rosso
hist_G = np.histogram(im_arr[:, :, 1].flatten()) # Distribuzione Verde
hist_B = np.histogram(im_arr[:, :, 2].flatten()) # Distribuzione Blu
features = np.concatenate((hist_R[0], hist_G[0], hist_B[0], hist_R[1], hist_G[1], hist_B[1]), axis=0)
features = np.reshape(features, (1, len(features)))
return (features)
# ------------------------------------------------------------------------------- #
# Evoca la funzione 'extract_features()' in loop. In R sarebbe meglio vettorizzare.
X = np.zeros((len(files), 63)) # ncol da modificare a seconda del'entrata
i = 0
for im in files:
feat = extract_features(im)
X[i, 0:len(feat[0])] = feat[0]
i += 1
print(i/len(files)*100, '%', ' done')
E alla fine, basta costruire un classificatore: in questo caso, data la semplicità dell’esempio, ho scelto una normale Random Forest. Facile da utilizzare avendo pochi parametri, non crea troppi problemi di overfitting e funziona straight out of the box.
# -------------------------------------------------------------------------------------------- #
# Stima del modello: Random Forest
print("Training")
# n_estimators is the number of decision trees
# max_features also known as m_try is set to the default value of the square root of the number of features
clf = RF(n_estimators=100, n_jobs=3)
scores = cross_validation.cross_val_score(clf, X, Y, cv=5, n_jobs=1) # Effettua la Cross Validation con 5 folds
print("Accuracy of all classes")
print(np.mean(scores)) # Stampa la media del punteggio di Cross Validation (accuracy in questo caso)
Se eseguite il programma, vedrete che l’accuracy media è di 1: abbiamo dunque costruito un modello perfetto per distinguere i colori di semplici immagini. L’accuracy di 1 tuttavia non è sempre un buon segno: potrebbe voler dire che il nostro modello è in over-fitting, ossia è troppo adattato ai dati osservati ma non è generalizzabile. In questo caso però non rischiamo di cadere in questo problema poiché il training set é molto semplice e praticamente privo di rumore.
Enjoy!
